Anmerkung: Dieser Artikel ist eine Ergänzung zum its-people-Webinar „Do you speak NLP – Ein Streifzug durch modernes Natural Language Processing mit Python“, gehalten im Oktober 2021 von Markus Zeeb und Uwe Blenz
Heute wollen wir uns mit dem Thema „Sentiment Analysis mit TF-IDF Classifiers“ beschäftigen. Dazu werden wir uns im ersten Teil allgemein mit TF-IDF befassen, die Grundidee dahinter beleuchten und Schritt für Schritt einen eigenen, kleinen TF-IDF-„Classifier“ implementieren (Python). Im zweiten Teil werden wir unsere Erkenntnisse aus dem ersten Teil nutzen, um einen weiteren TF-IDF-Classifier zu bauen und darauf trainieren, Produktreviews von Amazon.com in die Kategorien „positiv“ und „negativ“ einzuordnen.
Teil 1 – Kategorisierung von Texten
tf-idf steht für „term frequency – inverse document frequency“ und ist ein Verfahren, mit dem Texte (bzw. „Dokumente“) in verschiedene Kategorien eingeordnet werden können, bspw. Fachartikel nach Disziplin, Bücher nach Genre usw.
Allgemein gehen wir bei tf-idf davon aus, dass wir eine sehr große Sammlung von Dokumenten (linguist. „Corpus“ genannt) haben, die wir klassifizieren wollen; da es uns im Moment aber rein darum geht zu verstehen, wie tf-idf überhaupt funktioniert, nehmen wir für diesen Zweck folgenden, sehr übersichtlichen Corpus an:
In [1]:
documents = [
"foo bla bla foo",
"bla bla bar bla",
"baz bla bla foo bla bla baz",
"bla bla bla"
]
Unsere Aufgabe soll nun darin bestehen, die Dokumente (wenn möglich), den Kategorien „foo“, „bar“ und „baz“ zuzuordnen. Da unser Beispielskorpus lediglich aus 4 Dokumenten besteht, erkennen wir natürlich sofort, welche Dokumente in welche Kategorien gehören: Wir sehen bspw. sofort, dass der Term „foo“ zwei Mal in Dokument 1 enthalten ist und dieses folglich zur Kategorie „foo“ gehört. Interessanter wird es in Dokument 3, das zwei Mal „baz“ und ein Mal „foo“ enthält. Da wir die Zuordnung in mehrere Kategorien erstmal nicht erlauben, nehmen wir für Dokument 3 Kategorie „baz“ an, da „baz“ häufiger auftritt als „foo“.
Wir halten also fest:
Je häufiger ein Begriff (eng. „term“) in einem Dokument vorkommt, desto relevanter (bzw. „informativer“) ist er für dieses Dokument.
Diese Beobachtung stellt den Kern des tf-idf-Verfahrens dar und deshalb soll das erste Ziel auf dem Weg zu unserer kleinen tf-idf-Implementierung genau das sein: eine Liste pro Dokument, die angibt, wie oft (häufig) ein Begriff in diesem Dokument vorkommt:
In [2]:
import numpy as np
import pandas as pd
from typing import List, Set
def build_vocabulary(docs: List[str]) -> Set[str]:
vocabulary = set()
for doc in docs:
vocabulary = vocabulary.union(doc.split())
return vocabulary
def prepare_documents(docs: List[str]) -> pd.DataFrame:
vocabulary = build_vocabulary(docs)
results = []
for doc in docs:
vec = dict.fromkeys(vocabulary, 0)
for word in doc.split():
vec[word] += 1
results.append(vec)
return pd.DataFrame(results)
In [3]:
documents = prepare_documents(documents) documents
Out[3]:
| foo | bla | baz | bar | |
|---|---|---|---|---|
| 0 | 2 | 2 | 0 | 0 |
| 1 | 0 | 3 | 0 | 1 |
| 2 | 1 | 4 | 2 | 0 |
| 3 | 0 | 3 | 0 | 0 |
Wie wir sehen können, sind die Dokumente in unserem Corpus jetzt keine Texte mehr, sondern Listen, wie häufig ein Begriff in einem Dokument vorkommt (inkl. „0 Mal“, wenn ein Begriff also nicht im Dokument auftaucht).
Aus technischer Perspektive sind hier zwei Sachen passiert:
- Die Dokumente wurden vektorisiert, d.h. wir haben textuelle Daten in numerische Vektoren mit einheitlicher Länge überführt.
- Jeder Vektor ist gleichzeitig auch ein „bag of words“, in dem für jeden Term in unserem Corpus angegeben wird, wie oft er in einem bestimmten Dokumten auftaucht.
Theoretisch haben wir damit unser erstes Ziel auch schon erreicht: Wir haben nun für jedes Dokument eine Liste mit „term frequencies“, und tatsächlich arbeiten einige Implementierungen von tf-idf mit dieser Definition von „term frequency“.
Wir wollen uns damit aber noch nicht zufrieden geben und definieren „term frequency“ als „relative Häufigkeit“ von „absolute Häufigkeit eines Terms“ zu „Anzahl aller Terme eines Dokuments“:
In [4]:
def term_frequency(docs: pd.DataFrame):
res = []
for row in docs.values:
res.append(np.divide(row, row.sum()))
return pd.DataFrame(res, columns=docs.columns)
term_frequency(documents)
Out[4]:
| foo | bla | baz | bar | |
|---|---|---|---|---|
| 0 | 0.500000 | 0.500000 | 0.000000 | 0.00 |
| 1 | 0.000000 | 0.750000 | 0.000000 | 0.25 |
| 2 | 0.142857 | 0.571429 | 0.285714 | 0.00 |
| 3 | 0.000000 | 1.000000 | 0.000000 | 0.00 |
So weit, so gut. Meinen aufmerksamen Lesern wird aber sicher nicht entgangen sein, dass ich den „Elefanten im Raum“ bisher geflissentlich ignoriert habe, nämlich: „bla“.
Der Term „bla“ taucht mit Abstand am häufigsten auf und wenn wir uns stumpf an unsere Definition von „Relevanz“ weiter oben hielten, gehörten alle unsere Dokumente der Kategorie „bla“ an.
Das möchten wir natürlich unbedingt vermeiden und deshalb den „Relevanz-Score“ von Wörtern, die allgemein häufig (d.h. in vielen und unterschiedlichen Dokumenten) in einem Corpus vorkommen, weniger stark gewichtet werden als solche, die allgemein eher selten sind.
Um das zu erreichen, zählen wir erst einmal für jeden Begriff, in wievielen Dokumenten er vorkommt:
In [5]:
def document_frequency(docs: pd.DataFrame):
return docs.applymap(lambda n: 1 if n > 0 else 0).sum()
document_frequency(documents)
Out[5]:
foo 2 bla 4 baz 1 bar 1 dtype: int64
Das führt uns wieder zu einer Häufigkeit, dieses Mal nämlich die sogenannte „Dokumentenhäufigkeit“ (englisch: „document frequency“).
In dieser Form ist document frequency eine absolute Häufigkeit. Würden wir hierzu die relativen Häufigkeiten berechnen (d.h. durch die Gesamtzahl an Dokumenten in unserem Corpus teilen), ergäben sich die folgenden Werte:
In [6]:
document_frequency(documents).div(len(documents))
Out[6]:
foo 0.50 bla 1.00 baz 0.25 bar 0.25 dtype: float64
Diese Werte können wir so aber nicht als Gewichte verwenden, da sie immer noch nur solche Begriffe favorisieren, die über den ganzen Corpus hinweg häufig vorkommen. Erreichen wollen wir aber genau das Gegenteil!
Erinnern wir uns nochmal kurz an den Namen des Verfahrens: „term frequency – inverse document frequency“ — „Aha!“, wir nun der Lateiner rufen, „invers, von lat. inversus, also ‚umgedreht‘ oder ‚auf den Kopf gestellt‘! Könnte das die Lösung sein?“ Und tatsächlich, wenn wir die Relation einfach umdrehen und statt document frequency

einfach die „inverse document frequency“
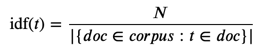
verwenden (mit |{𝑑𝑜𝑐∈𝑐𝑜𝑟𝑝𝑢𝑠:𝑡∈𝑑𝑜𝑐}||{doc∈corpus:t∈doc}| = „Anz. Dokumente, die t enthalten“ und 𝑁N = „Anz. Dokumente in Corpus“), drehen sich die Gewichtungen tatsächlich um:

Oder, weniger mathematisch als Python-Funktion:
In [7]:
def inverse_document_frequency(docs: pd.DataFrame):
frequencies = document_frequency(docs)
inverse_frequencies = pd.Series(len(frequencies), index=frequencies.index).div(frequencies)
return inverse_frequencies.apply(np.log)
inverse_document_frequency(documents)
Out[7]:
foo 0.693147 bla 0.000000 baz 1.386294 bar 1.386294 dtype: float64
Wobei wir in unserem Code einen zusätzlichen Schritt eingebaut haben, in dem wir den Logarithmus auf alle Häufigkeiten angewendet haben. Das hat den Grund, dass inverse Häufigkeiten sehr schnell sehr groß werden können. Insbesondere bei umfangreichen Corpora. Diese Entwicklung wollen wir mittels Logarithmus etwas dämpfen.
Außerdem hat es in unserem Fall den schönen Nebeneffekt, dass Begriffe, die in allen Dokumenten vorkommen (also sehr häufig sind), wegen 𝑙𝑜𝑔(1)=0log(1)=0quasi gecancelt werden 🙂
Und damit, liebe Leser, haben wir den Punkt erreicht, an dem wir nur noch die Teile zusammenzufügen brauchen, um den namensgebenden „Star“ unseres Artikels zu erhalten:
In [8]:
def term_frequency_inverse_document_frequency(docs: pd.DataFrame) -> pd.DataFrame:
return term_frequency(docs).mul(inverse_document_frequency(docs))
term_frequency_inverse_document_frequency(documents)
Out[8]:
| foo | bla | baz | bar | |
|---|---|---|---|---|
| 0 | 0.346574 | 0.0 | 0.000000 | 0.000000 |
| 1 | 0.000000 | 0.0 | 0.000000 | 0.346574 |
| 2 | 0.099021 | 0.0 | 0.396084 | 0.000000 |
| 3 | 0.000000 | 0.0 | 0.000000 | 0.000000 |
Das Ergebnis dieser Funktion können wir auch direkt verwenden, um die Dokumente in unserem Corpus zu kategorisieren:
In [9]:
def categorize(docs: pd.DataFrame) -> pd.DataFrame:
tf_idf = term_frequency_inverse_document_frequency(docs).to_dict('index')
for doc, record in tf_idf.items():
max_val = max(record.values())
key = '-'
if max_val > 0.0:
key = [k for k, v in record.items() if v == max_val][0]
tf_idf[doc]['category'] = key
return pd.DataFrame.from_dict(tf_idf, orient='index')
categorize(documents)
Out[9]:
| foo | bla | baz | bar | category | |
|---|---|---|---|---|---|
| 0 | 0.346574 | 0.0 | 0.000000 | 0.000000 | foo |
| 1 | 0.000000 | 0.0 | 0.000000 | 0.346574 | bar |
| 2 | 0.099021 | 0.0 | 0.396084 | 0.000000 | baz |
| 3 | 0.000000 | 0.0 | 0.000000 | 0.000000 | – |
Unsere 𝚌𝚊𝚝𝚎𝚐𝚘𝚛𝚒𝚣𝚎()categorize()-Funktion sieht zwar etwas wild aus, das Ergebnis kann sich aber sehen lassen: Für jedes Dokument haben wir den Term mit dem höchsten tf-idf-Score ermittelt und diesen als Kategorienlabel für das Dokument gewählt (bzw. „-“ falls kein tf-idf-Score größer 0 ist).
Übrigens haben wir die Labels der Dokumente streng genommen nicht vorgegeben, sondern unsere Funktion sie auswählen lassen. Tf-idf eignet sich daher auch hervorragend zur Exploration von unbekannten Corpora um zu sehen, in welche „natürlichen“ Kategorien die Dokumente darin fallen!
Das ist, wie gesagt, eine ungemein nützliche Eigenschaft des tf-idf-Verfahrens; in den meisten Fällen ist es aber umgekehrt und die Kategorien meistens grob schon vorgegeben. In dem Fall könnte eine Kategorisierung so aussehen, dass wir pro Kategorie einen festen Satz „typischer“ Begriffe bereits ermittelt haben und unsere categorize-Funktion dann lediglich anhand des häufigsten Begriffes entscheidet, in welche Kategorie ein Dokument fällt. Eine Kategorie „foo“ wird vermutlich den Begriff „foo“ als typischen Begriff deklarieren, weshalb Dokument 1 (bzw. 0) in unserem Corpus in diese Kategorie fiele.
Ein anderer Ansatz könnte sein, dass wir einen Teil der Dokumente eines Corpus „von Hand“ klassifizieren („labeln“) und ein ML-Modell darauf trainieren, die Kategorie eines Dokuments zu erkennen.
Diese Idee steckt hinter dem namensgebenden „Sentiment Analysis mit TF-IDF“, der wir uns allerdings erst im zweiten Teil dieser Serie zuwenden wollen – stay turned!
Bildnachweise: © pixabay_quantum-physics-4550602_1920





